Haskell that Nerdle

Nerdle is a fun number game, where you uncover the hidden equation by guessing numbers and operators. The goal is to make the fewest guesses possible to prove your arithmetical might! (My boss has a PhD in Physics so that last part didn’t go to plan. Your mileage may vary).

Check out Nerdle here

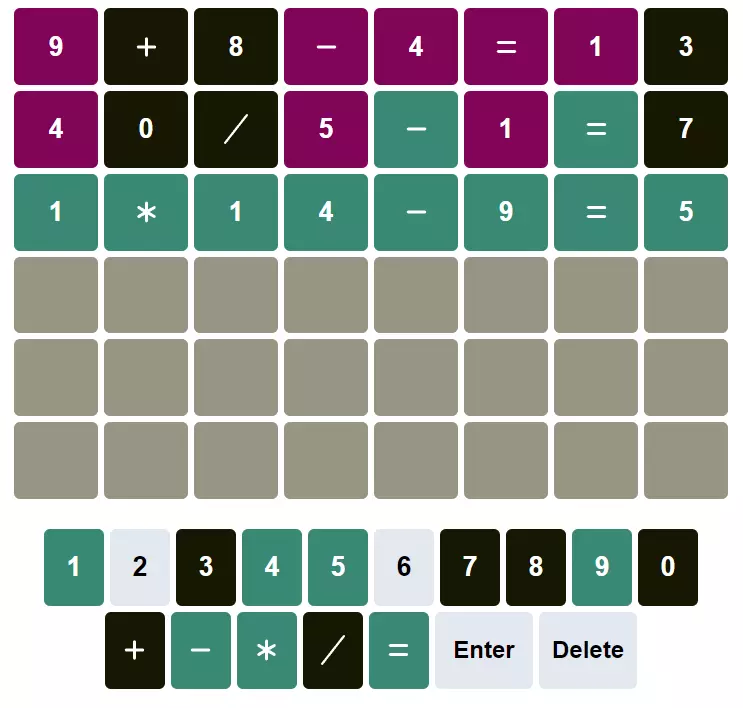
The First Game

Nerdle was first shown to me by a colleague at work, (I remain suspicious of their intentions). I started with a simple addition and it revealed some of the characters. Instead of thinking dilligently about the remaining possiblities, the quick and easy path of throwing equations at the wall won me over. Five blundering guesses later, I had the answer. Job done.

Just as it was with Minecraft, I had not yet realised the danger I was in…

The basic rules were now understood, and like the Moth to the flame, my mind could not resist the understanding that could be gleamed from my first game. I mostly managed to focus on my remaining work, but I needed to get home and think about the problem. My boss and coworker had both managed to solve it in three, balance had to be restored. Time was of the essence, a new Nerdle puzzle is generated every day, and I would not be content with a five guess solution.

A “Better” Way

Should your first guess include a single operator, two, three… Is three even possible?

The importance of the first guess seemed intuitively obvious. You want to uncover the most information possible. There is a set of all valid equations that can be made from eight characters. The goal of our first (and every) guess is to reduce the number of remaining valid equations as much as possible.

My first port of call was the ‘=’ sign. There are three valid positions. Single, double and triple digit answers are all possible. This means our equals sign can be in position, 5, 6 or 7 (forgive me for indexing from 1). Already this restricts our equations to one of three forms.

1. _ _ _ _ _ _ = u
2. _ _ _ _ _ = tu
3. _ _ _ _ = htu

I decided that my first guess would be for the two digit answer, as I suspected this was the most common case. We wil look at the numbers shortly and learn if this is indeed the case.

The legal operators we have in Nerdle are / * + -. There is a lot to discuss here.

First consider our chosen equation form where an answer must be two digits. The left hand side of our equation must be one of the following forms, where ‘o’ represents an operator.

1. _ o _ _ _ = tu
2. _ _ _ o _ = tu
3. _ o _ o _ = tu
4. _ _ o _ _ = tu

Multiply is looking very unlikely. Try plugging numbers into these forms to get a two digit answer, you’ll find it’s not very common. There is the special multiply by zero case, however we cannot use that to get a two digit answer using any of the forms we have.

Division is also looking very unlikely. It’s only possible in the second and third case, but in both of these there are not many valid answers. This is because division has a caveat in Nerdle. Divisions must have no remainders. This seriously reduces the valid divisors we can use. There is also the divide by zero edge case which is not allowed, perhaps a reason to not guess zero if you know there is a division?

Addition may also be on the ropes. The first two cases involving a three digit number can both be ruled out as they would necessitate a three digit answer. However, the final two cases have valid answers purely using addition. The final case in particular has many valid answers using addition, so on reflection, perhaps addition is a wise choice.

Subtraction is in a similar place to addition. The second form has some solutions but again the final form has the most.

It’s worth remembering at this point that all of this thinking is assuming we know where the equals is. If we have made our first guess, we will know some of the numbers that either can or cannot exist. This massively impacts the likelihood of different forms. You cannot simply memorise the information above. For every piece of information you have, you need to figure out which forms and numbers are most likely.

The Numbers…

The above is all well and good. I’ve solved all subsequent puzzles in three guesses using this kind of reasoning, but it’s slow. Human intuition is also very suspect. My normal first guess is 9 + 8 - 4 = 13. It’s worked well for me so far, but is it optimal? Almost certainly not.

The above guess was based mostly on vague assumptions, a desire to test for two operators, and the hope that the two digit answer is the most common case.

To get to the bottom of this, and as an excuse to play with Haskell again, I decided to write a program to help me solve Nerdle puzzles. We will look at the program in more depth later, but here is the TLDR.

I first attempted to generate every possible eight character string using some basic rules to reduce the amount of garbage strings. This initially took two minutes to run, resulted in a 400MB file, and a huge number of invalid equations, not ideal.

I managed to get this under 100MB with smarter rules, but it was still terrible, and I had problems with zero appearing at the start of multi digit numbers. Suddenly, I remembered the teachings of the legendary Dr Dave Harrison, former Professor of Computer Science at Northumbria University. The module I was remembering was infamous among the students, “Compiler Writing”.

The first step of writing a compiler is Tokenisation. You convert your input Strings into tokens, objects that are easier for your program to deal with. I converted my expression generator to be token based, and bang, a file under 0.5MB with valid looking expressions.

Now I have my program, I can quickly hack in some debug code and actually count the possibilities. Let’s see what happens. Really lets see, at time of Writing, I haven’t done this bit yet. Just give me some Coffee and half an hour please…

…Right then

I first had to modify my code to generate only number tokens on the right hand side of equals. Initially I was allowing expressions with operators, however I’ve yet to see a Nerdle solution with operators on both sides, so for the remainder of this article, I will make the assumption that Nerdle only allows the right hand side of the equation to be a single number.

It’s worth noting that Nerdle may restrict the equations further when it generates puzzles, to avoid boring multiply by zero cases and similar gameplay situations. I cannot account for this as I don’t have the source code, so I will include all possible valid equations.

Okay, I’ve hidden the answer long enough. Assuming my code is correct, which is the biggest assumption we’ve made so far, here are the details (The generated list is now 256KB, which is a very satisfying coincidence).

1. There are 29042 possible solutions to Nerdle
2. There are 16856 single, 10868 double and 1318 triple digit answers in the set
3. Multiply is surprisingly the most common operator. Addition and Subtraction are roughly half as probable, while divide is significantly less probable

That is the summary, I’ve included the exact frequencies below in case you desire them for your own use.

PossibleSolutions    : 29042
SingleDigitSolutions : 16856
DoubleDigitSolutions : 10868
TripleDigitSolutions : 1318

Operator Frequency
* : 21918
+ : 11976
- : 10926
/ : 4148

Digit Frequency
0 : 25555
1 : 18708
2 : 15573
4 : 14413
3 : 14130
5 : 13697
6 : 13664
8 : 13143
7 : 12747
9 : 12696

Conclusions

Wow. There are quite a few surprises here.

Firstly, it seems that single digit answers are the most common, so that conflicts with my current initial guess. It also seems that multiply is by far the most common operator. This really surprised me, however there is a big caveat here. There are over 6000 cases of multiply by zero.

If nerdle equations are random and allow this, then the optimal guess may well include a multiply and zero somewhere. It’s also worth noting, that the majority of these cases were for single digit answers, which makes the disparity between the single and double digit case far smaller.

I suspect, but can’t prove, that the digit frequency means it’s likely not worth repeating a digit in an initial guess. Damnit Jim, I’m a Software Engineer not a Mathematician. Now that I have the data, I’m tempted to spend more time trying to analyse it, but for now, it seems only prudent to come up with a new initial guess, and try it on todays Nerdle.

I want this guess to include a multiply, a zero, and by necessity probably a subtraction in order to achieve a single digit answer.

4 * 3 - 12 = 0 Seems legit. It includes all of the most common digits, it gives me the important multiply, the zero. Lets test this bad boy out!

Wow. It was incredibly Lucky to get the exact form of the equation first time. Rather interestingly, none of the most common digits are present. This is actually a good thing, as it allows us to rule out a huge number of possibilities. Lets see what my program says. 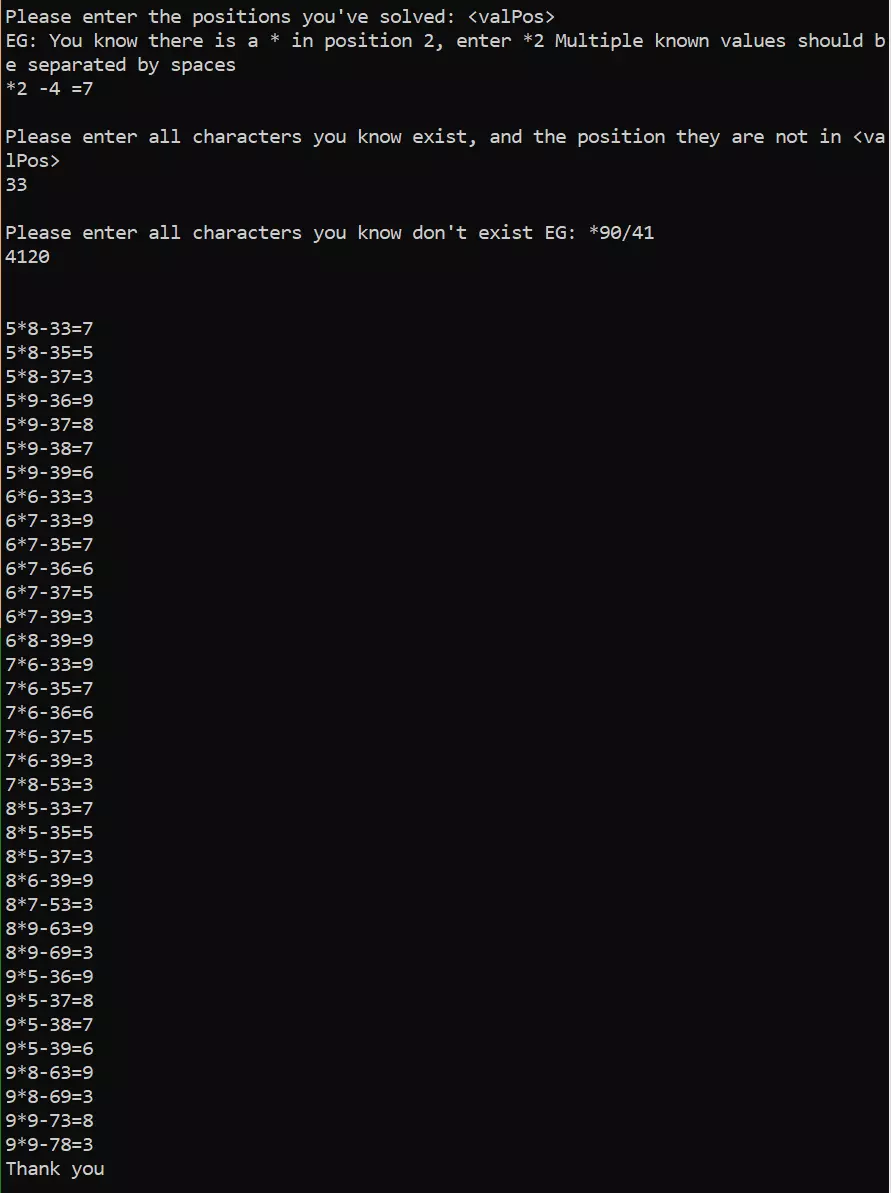From 29042 possibilites down to 35 options. Not bad for a weeks work. The number of options is thankfully small enough to fit into one image, but also it reveals a weakness of my program.

Currently, my program doesn’t tell you which of these is the next best guess, so we’ll have to wing it manually with a little reasoning.

Notice that the majority of the answers include a 3 after the minus. It is more likely for the answer to be one of these. The digit after that looks to be a tossup between 7 and 9, so we will use the answer digit to help inform our choice. Again, it is mostly a toss up between 7 and 9, so we want to try and include these in our final guess.

At this point it’s hard to avoid duplicate digits. Let’s try 7 * 6 - 39 = 3 It’s probably not the right choice, but I don’t have all day, so lets roll those dice.

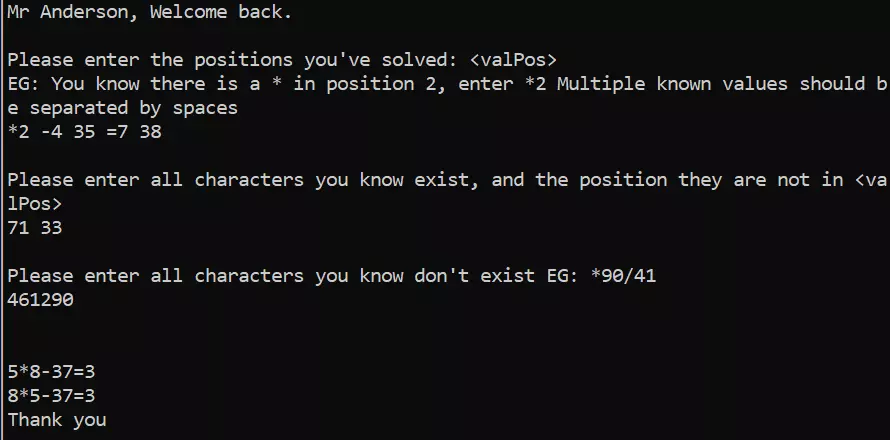
It’s at this point you ask yourself, do you feel lucky Punk? We have two remaining options. Since I have no information about digits five or eight so far, this is going to be a complete guess. I generally take the side of order as opposed to chaos, so lets pick the first equation my program spat out 5 * 8 - 37 = 3

Drum Roll Please…

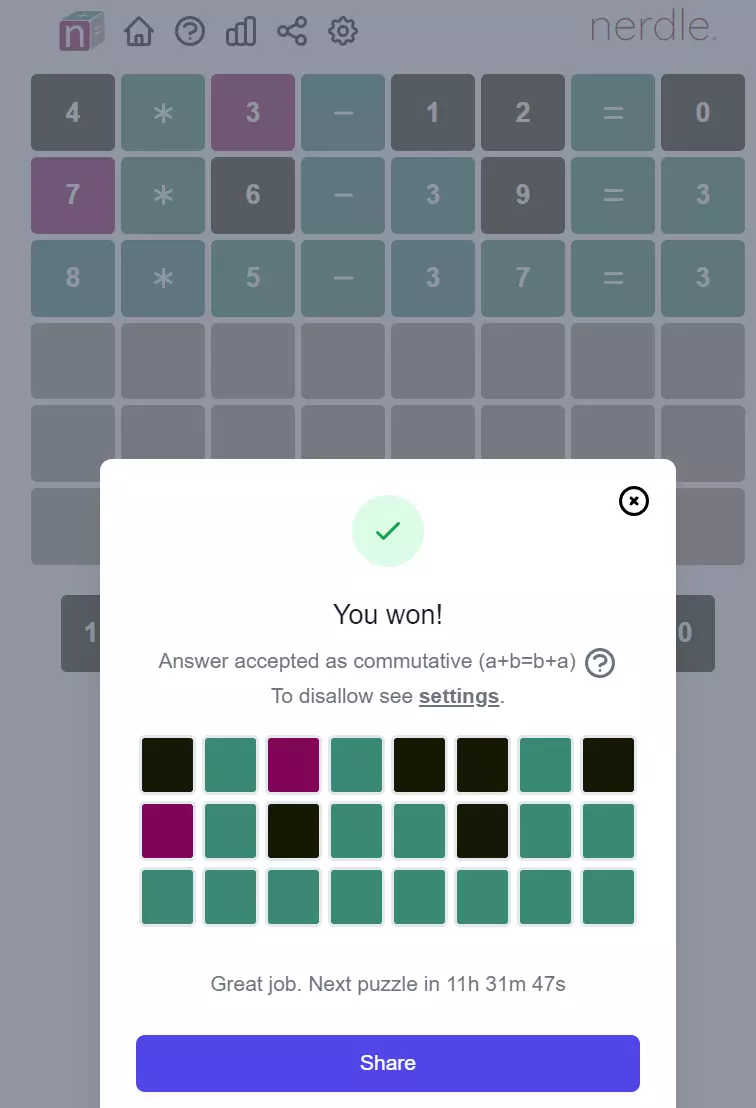
Awesome! I had a whole host of expletives prepared, but we pulled through and maintained our track record of three guesses using the program.

Just a moment “Answer accepted as commutative”. I don’t recall seeing that before. It sounds like it would have accepted either of my answers. Perhaps there is room for optimisation here.

It’s worth noting that my old starting guess would also have performed well here. It would have gotten the minus, and crucially the final digit of the answer, which is often incredibly helpful. The key would have been figuring out if I was dealing with an initial three digit number, or another operator.

This topic is perhaps worth an improved program and second post, but I suspect I’ll be onto other things by then. To sum up this rather long post, lets take a look at the program and how it works. I want to stress that I’m a Haskell newbie, and I would not recommend using this code for learning purposes.

Show Me The Haskell

I’ve published this tool on github under the MIT license, feel free to do whatever you want with it.

The program really has three main parts.

1. Generate all possible token expressions
2. Ability to evaluate an expression
3. User input/output to filter on available data

Generating Tokens

Let’s start with a top down view. We have the high level function “buildAllEquations”.

buildAllEquations :: [TokenEquation]
buildAllEquations = concatMap buildEquations ofLegalSizes

This creates a list of all equations, ignoring whether the left and right hand sides are equal. We are mapping over ofLegalSizes, which is a list of tuples that contains the number of characters on the left and right hand sides, eg (5,2) for the two digit answer case.

“buildEquations” is the function that creates all possibilities for a given legal size, so lets take a look.

buildEquations :: (Int, Int) -> [TokenEquation]
buildEquations (left, right) =
    [(lh, rh) | lh <- (buildExpressions left left []), rh <- (map (\x -> [x]) (buildNumberTokens [right]))] 

If that line of code looks completely alien, it may be worth reading about List Comprehensions. Ultimately, it is returning a list of tuples. The first and second item in the tuple respectively represent the left and right hand expressions in the equation. This list comprehension creates a tuple for every possible combination of these values.

The right hand side is not that interesting, it simply builds an expression, which contains a single token. The token is a number value with the specified number of digits.

Now the real work begins. Lets dive into the left hand side, “buildExpressions”.

-- Builds all possible expressions of a given length, whether they are valid or not
buildExpressions :: Int -> Int -> TokenExpression -> [TokenExpression]

This has some strange syntax if you’ve never done any Haskell, so lets walk through it. We have a recursive function. It takes the remaining number of characters we have to work with, the maximum characters in total available for this expression, and the expression we have built so far.

buildExpressions remaining maxLength acc
    | remaining < 0 = [acc] -- Should never happen but I'm paranoid

The pipe character is a guard in Haskell. It’s a paranoia check for if we somehow have a negative value for remaining characters. If this happens, we just return the expression so far. We could change it to <= and it would actually remove the need for the next line.

buildExpressions 0 maxLength acc = [acc]

This is the intended escape from the recursion. If there are no remaining characters, we return the expression we have.

buildExpressions remaining maxLength acc = do
    let values = buildNextTokens prev remaining 
    concatMap (\x -> buildExpressions (remaining - getLength x) maxLength (acc ++ [x])) values
    where
        prev = if (length acc /= 0) then Just (last acc) else Nothing 
        index = length acc

This is where the fun begins. First note the “where”. We are giving names to two expressions. Prev is a Maybe value for the previous token, index is simply the length of our expression so far. The Maybe is a deep rabbit hole. If it helps, you can think of it as an alternative to null. A Maybe value is either Just a value, or it is Nothing.

The first line builds a list of all possible tokens that can come next, and assigned it to values. The second line is the tricky part. Here we map recursively over the function for each allowed next token. This creates a tree of sorts, producing all possible values. The concat part is important. This flattens our output so we ultimately end up with a single list of expressions, not some crazy tree structure.

So all together, the function looks like this.

-- Builds all possible expressions of a given length, whether they are valid or not
buildExpressions :: Int -> Int -> TokenExpression -> [TokenExpression]
buildExpressions remaining maxLength acc
    | remaining < 0 = [acc] -- Should never happen but I'm paranoid
buildExpressions 0 maxLength acc = [acc] 
buildExpressions remaining maxLength acc = do
    let values = buildNextTokens prev remaining 
    concatMap (\x -> buildExpressions (remaining - getLength x) maxLength (acc ++ [x])) values
    where
        prev = if (length acc /= 0) then Just (last acc) else Nothing 
        index = length acc

We could keep going, but my goal here is to give a general overview of the program. If you want to look at it, feel free to have a look at the github link at the start of this section.

Evaulate An Expression

We call the buildAllEquations function that we just took a look at here.

let validEquations = filter equalityCheck buildAllEquations

Notice we are filtering over the results with a function called equalityCheck.

-- Check if an equation is correct
equalityCheck :: TokenEquation -> Bool
equalityCheck equation = if isNothing left || isNothing right
    then False
    else areIntsEqual left right 
    where
        left = evaluateTokens (fst equation)
        right = evaluateTokens (snd equation)

Equality check takes in an equation and returns the Boolean value True if it is valid, False if it is not. The isNothing check is performed on each side of the equation. If something went wrong during the expression generation phase, a Nothing will be returned. We are simply returning False if either expression is Nothing. A better solution here would be to make use of the Either Monad and log some errors.

We then compare the values on both sides of the equation, but these have not yet been calculated yet. Again we look at the “where” keyword. Here we call evaluateTokens on each side of the equation. This is the function that actually does the maths and reduces our expression to a single number token.

-- recurse over operators
evaluateTokens :: [Token] -> Maybe Int
evaluateTokens tokens 
    | (length tokens) == 1 =
        if isValue token
            then Just (getValue token)     
            else Nothing 
    | isNothing op = Nothing
    | otherwise = do
        operator <- op
        let index = snd operator
        if not (isOperatorIndexValid tokens index) then Nothing
        else do
            let res = performCalculation (tokens !! index) (tokens !! (index - 1)) (tokens !! (index + 1)) 
            if isNothing res then Nothing 
            else 
                evaluateTokens (concat [take (index - 1) tokens, [fromJust res], drop (index + 2) tokens]) 
    where
        token = head tokens
        op = findPriorityOperator 0 Nothing tokens

Okay. This is a big one. Congratualtions on making it this far.

Lets start with the definition. The function takes a list of tokens and returns a Maybe Int. If we see a Nothing being returned, it means something has gone wrong, and as mentioned earlier, it will be filtered out of the valid equations list.

This function calls itself recursively. We first check if our tokens list only contains a single token. This is to handle the case of having a single value at the end, which is the integer we are after. If the token is indeed a value, we return the value inside a Maybe using the Just constructor for the Maybe type. If the token is not a value, then it must be an operator, in which case we return a Nothing as an error, because a lone operator is not a valid expression.

The main body of the function is concerned with finding the operator with the highest precedence (multiplication before subtraction and so forth). While there are operators in the token list, we find the first one to execute, and apply it to the number values either side of it. If all goes well, we recursively call our function again, replacing the operator token and it’s two value tokens with a new value token which represents the result of the operation. In this fashion, we gradually arrive at a list containing only a single value token, our answer.

User Input

The user input and output is fairly straight forward, and shouldn’t be too confusing. Like other languages we write to the console, read from the console, valdidate the input, and do something with it.

getUserInputData :: IO (Maybe KnownData) 
getUserInputData = do
    putStrLn "Please enter the positions you've solved: <valPos>"
    putStrLn "EG: You know there is a * in position 2, enter *2 Multiple known values should be separated by spaces"
    knownChars <- getLine
    putStrLn "\nPlease enter all characters you know exist, and the position they are not in <valPos>" 
    missingPosition <- getLine
    putStrLn "\nPlease enter all characters you know don't exist EG: *90/41"
    excluded <- getLine
    putStrLn "\n"
    let vKnownChars = validateCharsWithPos knownChars
    let vMissingPositions = validateCharsWithPos missingPosition
    let vExclude = validateChars excluded

    if isNothing vKnownChars || isNothing vMissingPositions || isNothing vExclude
        then return Nothing
        else 
            return (Just (KnownData (fromJust vKnownChars) (fromJust vMissingPositions) (fromJust vExclude)))

This function has an interesting type. It has no input parameters, but returns an IO (Maybe KnownData). The IO monad is haskells, way of handling side effects. We are reading user input which could be anything, so under normal circumstances our function would be impure. Again we are using the Maybe type. If the user provided data is invalid, we return an IO Nothing.

After the user input and output, we have three validation functions. Each one validates user input. If any of them fail, we return Nothing from the overall function, and the user has to start again (Quality ux I know. I’m operating under the assumption that the user is always right).

Assuming the user didn’t f*** up, we reach the final step of filtering our valid equations based on the data provided by the user.

-- Filter all equations using provided guess data
stringEquationsFromGuess :: Maybe KnownData -> IO (Maybe [String])
stringEquationsFromGuess Nothing = return Nothing
stringEquationsFromGuess (Just (KnownData known position exclude)) = do    
    let validEquations = filter equalityCheck buildAllEquations
    let sEquations = map stringEquation validEquations
    -- The first thing has to be a filter or we get no where....
    let one = filter (\e -> isNothing (elemIndex False (map (\k -> (filterFromKnown e) k) known))) sEquations
    -- Filter out chars at positions we know cannot exist, and equations missing known cars
    let two = filter (\e -> (isSubset (map fst position) e)) one 
    let three = filter (\e -> (allowedAtPos position e)) two

    -- Filter out equations with chars missing
    let four = filter (\e -> (hasNoExcludedChars exclude e)) three
    return (Just four)

The start of this should look familiar. Once again we build our valid equations, but now we stringify them, to make it easier to filter using the user’s guess.

The terribly named variables, one, two, three and four, each represent the previous result with an additional filter applied. This is awful code, and I feel some shame, but it is what it is.

Fin

That was an unexpected journey. I hope you found something of interest in this post. A very small part of me still feels the need to write a compiler, and this project made me think about that. On the other hand, x86 assembly? Think I’ll pass.

Bye for now.